|
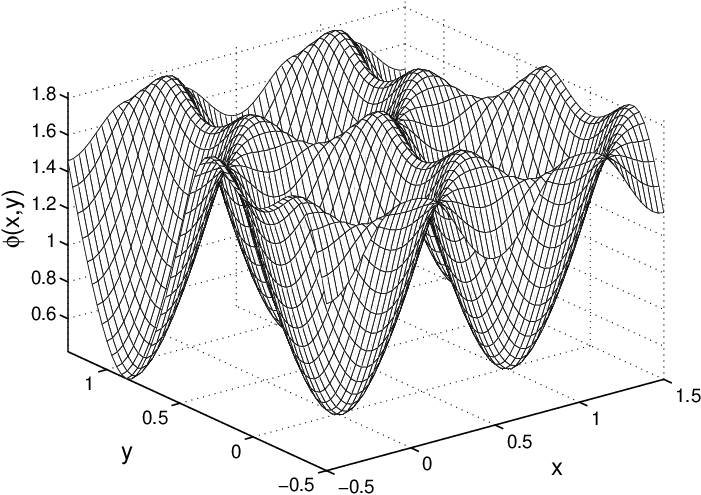
The electrostatic potential in a superconductor is studied. To this end Bardeen’s extension of the Ginzburg-Landau theory to low temperatures is used to derive three Ginzburg-Landau equations—the Maxwell equation for the vector potential, the Schrödinger equation for the wave function, and the Poisson equation for the electrostatic potential. The electrostatic and the thermodynamic potential compensate each other to a great extent resulting into an effective potential acting on the superconducting condensate. For the Abrikosov vortex lattice in niobium, numerical solutions are presented and the different contributions to the electrostatic potential and the related charge distribution are discussed. see the paper Electrostatic potential in a superconductor P. Lipavský, J.Koláček, K. Morawetz, E.H.Brandt |
Electrostatic potential in Nb superconductor with vortex lattice
temperature: t = T/Tc = 0.5 |
|